10112. Tree Сбалансированное дерево

Дано бинарное дерево. Определить, является ли оно сбалансированным. Бинарное дерево является сбалансированным, если глубина его поддеревьев (левого и правого) отличается не более чем на 1.

Определение дерева:

//Java

class TreeNode {

int val;

TreeNode left;

TreeNode right;

TreeNode(int x) {

val = x;

left = null;

right = null;

}

}

// C++

class TreeNode

{

public:

int val;

TreeNode *left;

TreeNode *right;

TreeNode(int x) : val(x), left(NULL), right(NULL) {}

};

Реализуйте функцию isBalanced которая возвращает true если дерево является сбалансированным и false иначе.

// Java

int isBalanced(TreeNode tree)

// C++

int isBalanced(TreeNode *tree)

Пример

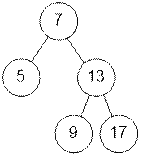
Функция isBalanced возвращает true так как дерево является сбалансированным.

РЕШЕНИЕ

дерево

Анализ алгоритма

Пусть Height – функция, которая возвращает высоту дерева (количество вершин от корня до самого дальнего листа). Однако если дерево не сбалансировано, то функция Height возвращает -1.

Для каждой вершины root следует вычислить:

· высоту левого поддерева Left;

· высоту правого поддерева Right;

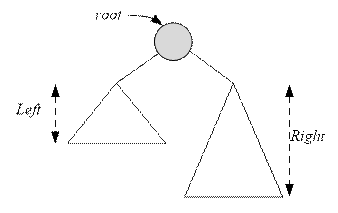
Если одно из значений Left или Right равно -1, то дерево root не сбалансировано. Дерево root также не будет сбалансировано, если | Left – Right | > 1.

Исходное дерево root будет сбалансированным, если его высота не равна -1.

Реализация алгоритма

bool isBalanced(TreeNode* root)

{

return (Height(root) != -1);

}

Если дерево root не сбалансировано, то функция Height возвращает -1.

Если дерево root сбалансировано, то функция Height возвращает высоту дерева (количество вершин от корня до самого дальнего листа).

int Height(TreeNode* root)

{

Если root = NULL, то высота дерева равна 0.

if (root == NULL) return 0;

Вычисляем высоту левого Left и правого Right поддерева.

int Left = Height(root->left);

int Right = Height(root->right);

Дерево не сбалансировано, если выполняется одно из следующих условий:

· левое поддерево не сбалансировано (Left = -1);

· правое поддерево не сбалансировано (Right = -1);

· модуль разницы глубин поддеревьев больше 1.

if (Left == -1 || Right == -1 || abs(Left - Right) > 1) return -1;

return max(Left, Right) + 1;

}

Java реализация

boolean isBalanced(TreeNode tree)

{

return (Height(tree) != -1);

}

int Height(TreeNode tree)

{

if (tree == null) return 0;

int Left = Height(tree.left);

int Right = Height(tree.right);

if (Left == -1 || Right == -1 || Math.abs(Left - Right) > 1)

return -1;

return Math.max(Left, Right) + 1;

}